CRC 被广泛应用于检测数据传输错误。它将数据视为一个长的二进制数，并利用特定的生成多项式进行除法运算，从而计算出校验值。CRC能够高效地检测出常见的错误类型，包括单比特错误、双比特错误以及突发错误。需要注意的是，CRC只能用于检测错误，而无法用于纠正错误。

CRC 有很多不同的标准和协议，每种标准或协议都规定了自己特定的生成多项式。这些生成多项式是预先定义好的，并且在发送方和接收方之间必须一致使用。

计算过程

假设

• 原始数据：10110

• 多项式：G(x) = x^4 + x + 1，最高阶r为4

在原始信息后追加最高阶r个0作为被除数

• 原始数据：10110

• 补充 4 个 0 后的被除数：101100000

由多项式得到除数

• 多项式 G(x) = x^4 + x + 1

• 从高到低列出所有可能的指数，并判断每一项是否存在：

  • x^4：存在，系数：1

  • x^3：不存在，系数：0

  • x^2：不存在，系数：0

  • x^1：存在，系数：1

  • x^0：存在，系数：1

• 因此，除数为：10011

生成CRC校验码

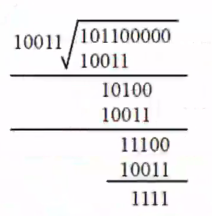
模2运算即异或运算，也就是相同为0，不同为1。当余数位数不足最高阶r位时，在余数左侧补0。计算过程如图

• 被除数：101100000

• 除数：10011

• 余数（CRC校验码）：1111

生成最终发送的信息串

将CRC校验码追加到原始信息后面。

• CRC校验码：1111

• 最终发送信息串：10110 1111

数学知识补充

多项式中的指数

• 指数（次幂）：指一个数被自身乘的次数。

• 多项式的每一项：由一个系数、一个变量和一个指数组成。

例如，在多项式 G(x) = 4x^3 + 3x^2 - 2x + 1 中：

• 4x^3：系数是4，变量是 x，指数是3。

• 3x^2：系数是3，变量是 x，指数是2。

• -2x：系数是-2，变量是 x，指数是1（尽管通常省略不写）。

• 1：常数项，可以看作 1x^0，系数是1，指数是0。

多项式中的最高阶

• 最高阶：多项式中所有项中指数最大的那一项的指数。

• 例如，在多项式 G(x) = 4x^3 + 3x^2 - 2x + 1 中，最高阶是3，因为 4x^3 的指数最大，为3。

多项式x所有可能的指数

• 对于任何非零的 x，x^0 的值总是1。

• 多项式中所有可能的指数是从 x^0 到 x^最高阶，即 x^0, x^1, x^2, ..., x^r，其中 r 是最高阶。

用于CRC校验的二进制形式系数

• 存在：系数为 1

• 不存在：系数为 0

检查每一项的存在性并记录二进制形式的系数

例如，对于多项式 G(x) = x^3 + x + 1：

1. 列出所有可能的指数：

   • x^0, x^1, x^2, x^3。

2. 检查每一项的存在性并记录系数：

   • x^3 存在，系数为1。

   • x^2 不存在，系数为0。

   • x^1 存在，系数为1。

   • x^0 存在，系数为1。

3. 形成二进制形式：

   • 从最高次幂到最低次幂排列，得到二进制序列为 1011